Central Limit Theorem and Convergence
This is my first post (yaaay \o/).
Sometimes it’s hard to understand the meaning of CLT and convergence. I realized many times when people first hear about these concepts that they actually don’t know what it’s. And they stay this way until they learn (if they learn) more advanced theories.
One of the first things that we learn in school is Central Limit Theorem. Basically for any symmetric distribution, when you have a large number of observations, it converges to a normal distribution.
There are some distributions more inclined to converge than others. For example, the exponential distribution, t-student, binomial.
But those are all old news. Here I’m going to show an example of convergence in real life.
Exponential Distribution
The CLT says that if you have X_1, X_2, ...X_k independent random variables with distribuition exp(\lambda) when k is large enough the mean of these identical distribuited vectors converges to a normal with mean \(\lambda\) and variance 1/(k*\lambda^2).
Now to prove this, we can generate 40 observations from a exponential distribuition with \lambda = 0.2. And then replicate this experiment k times.
The Rcode for that is:
k=10 #number of replication
n= 40 #size of each vector
lambda = 0.2
list_of_exponential = array(1:k) #variable to keep all the calculated means
#loop to run the replication
for(i in 1:k){
list_of_exponential[i] = mean(rexp(n, lambda))
}
As you can see the k here is very small (10) so how would be the distribution of the mean for these iid variables?
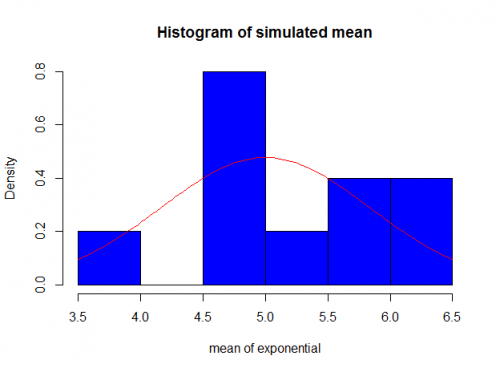
As you can see it’s not very “normal”. The reason for that is because we need a bigger k in order to get closer to a normal.
If we run the same script with k=100 for example
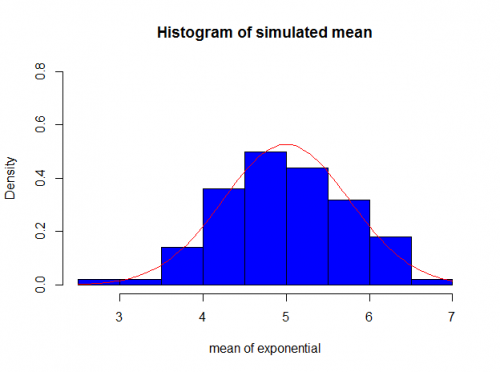
And if we run for k=1000
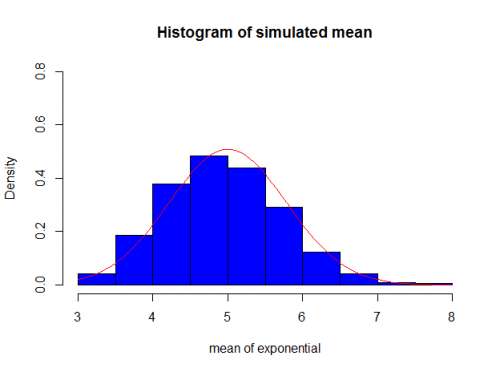
You finally can see that it does converge to a normal distribution.
There some decent explanation in the wikipedia page (if you need more theory) and I also included the code in my github page.
As this is my first post, please send me your feedback/suggestions so I can improve the blog and posts =D.